1146 Topological Order

题目

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.
Output Specification:
Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.
Sample Input:
6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6    
Sample Output:
3 4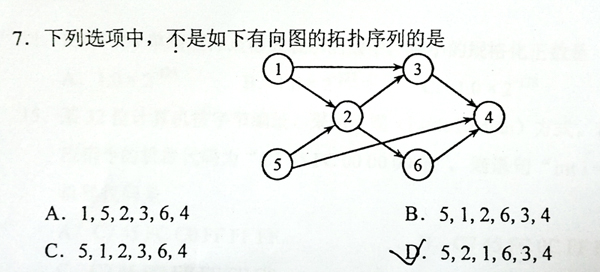

词汇

topological order：拓扑排序

分析

本题和上一题一样，都是单纯的考察数据结构知识，这次是有向无环图的拓扑排序问题。

拓扑排序

拓扑排序，从概念上来说就是由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。（不是太好理解。。就不解释了），如何判断一个图是否拓扑有序并得到一个图的拓扑排序呢？只要遵循以下步骤即可：

1. 在图中选择一个入度为0的节点；
2. 删除该节点以及所以从该节点出发的边。（删除的顺序即为该图的一个拓扑排序）
3. 重复上述操作，直到全部顶点被删除，或者不存在入度为0的节点。此时如果还有节点存在，说明该图非拓扑有序（存在环）。

根据题意，我们不需要构建一个图的拓扑排序，我们只需要判断给出的排序是否是拓扑有序即可。那么判断的方法也很简单，对于序列的每个点，我们都判断它的入度是否为0，如果为0，删除其节点和相应的边；如果最后还有节点存在，则说明这不是一个拓扑排序。当然这里也存在技巧，即我们可以单独记录一个indegree数组来记录每个点的入度，将删除边的操作转化为将对应定点入度减一即可。

代码

#include<iostream>
#include<vector>

using namespace std;

int main(){
    int N, M;
    cin >> N >> M;
    // 这里需要注意一下 这里声明的是一个二维数组
    // 另一种比较直观的二维数组声明方法是vector<vector<int> > g(n, vector<int>(n, 0)) 声明一个nXn的全0数组
    //但是这种方式速度较慢 代码中这种方式声明速度上会快一些。（因为这个原因代码超时
    //同时作为邻接表，由于只需要用到以这个点为起点有哪些边 所以不需要完整建出二维矩阵
    //只需要按需讲需要的点push_back
    vector<int> g[1001];
    int in[1001]; // 存每个点的入度
    for(int i=0; i<M; ++i){
        int x, y;
        scanf("%d %d", &x, &y);
        g[x].push_back(y);
        in[y] += 1;
    }
    int k;
    cin >> k;
    int flag = false;// 用于判断是否加空格
       for(int i=0; i<k; i++){
        int judge = 1; // 用于判断是否为拓扑排序
        vector<int> tmp_in(in, in+N+1); // 复制一个in数组
        for(int j=0;j<N;j++){
            int a;
            scanf("%d", &a);
            if(tmp_in[a] != 0){ //判断入度
                judge=0;
            }
            for(auto it: g[a]){
                tmp_in[it] -= 1; // 将以a为起点的边全部删除（相应点入度减一）
            }
        }
        if(judge==1){ // 是拓扑排序 跳过即可
            continue;
        }
        printf("%s%d": flag==1?" ", "", i);
        flag = true;
    }
    return 0;
}